For the past few months, I have been practicing for the NWERC 2020. During my practice I came across a beautiful tool for visualizing computational geometry: Geo Debugger. This is a small library for c++ (only a single .h file) that you can include and immediately use. With simple statements you can make lines, points, circles and more in the visualization. When the c++ program is done, the output is stored in a html webpage, which displays the result. Because geometry problems are frequent in the ICPC contests, and because of this tool, I wanted to really dig into geometry problems. In this blog I will share the cool visualizations I made during my practice:
| Problem | Original Problem statement | Visualization |
|---|---|---|
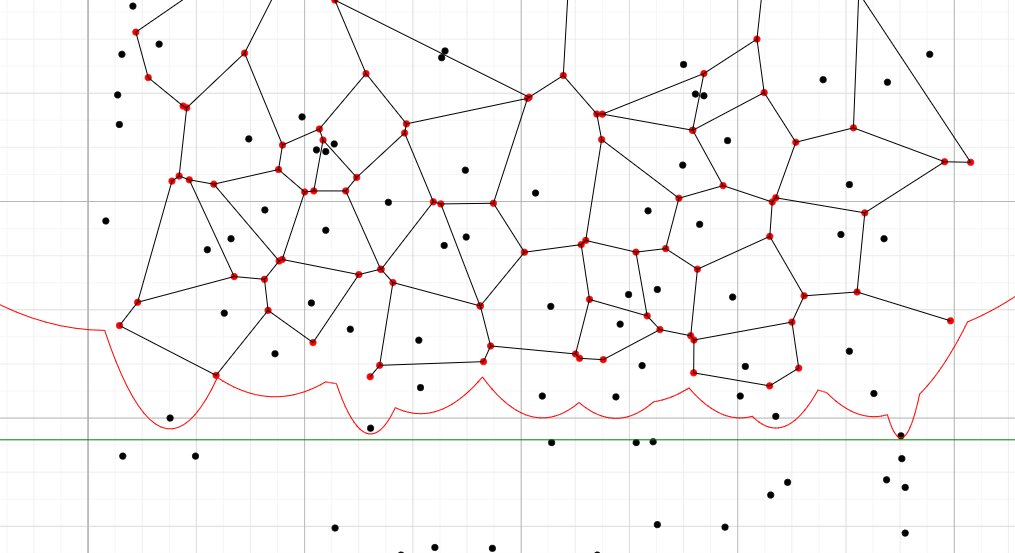
| Voronoi | Calculate the Voronoi Diagram of a set of points in 2D in O(n log(n)), using Fortune’s Sweep. | Voronoi. For this visualization it’s best to turn on “free camera” |
| Triangulation | Calculate the triangulation of a simple polygon in O(n^2) using the earcutting algorithm. | Earcutting Triangulation |
| Radial Sweep | Given a set of convex polygons and a point inside a bounding square, calculate the amount of integer points of the bounding square you can see. Runs in O(R log(R) + N + P), where N is the side length of the bounding square and R is the amount of polygons and P is the sum of the point counts of all polygons. This was a problem from the 2003 IOI (International Olympiad in Informatics): See here for the original problem: https://dmoj.ca/problem/ioi03p6 | Radial Sweepline |
| Convex Holes | Given a set of points, calculate the convex hole with the largest area. A convex hole is a convex polygon with all its vertices being input points and none of the input points lie inside the polygon. This is a problem from project Euler. See: https://projecteuler.net/problem=252 | Convex Holes |
| RC Kaboom show | There are a couple of objects beginning at different positions and each object has a constant speed in a certain direction. Some objects move faster than others. We want to know what is the first time that an object comes across the trail of another object. The original problem statement was a bit different and can be found here: https://codeforces.com/problemset/problem/1359/F. The basic idea of the solution is: Binary Search the answer. Say we pick a time T and we want to know if some object crossed the trail of another object. At a certain time we can easily calculate all trails as a set of line segments. Now the task boils down to finding whether there exists an intersection in this set of line segments. This can be done in O(n log(n)) with a sweep line. | RC Kaboom Show |
| Laser | Calculate the number of bounces a laser makes inside of a elliptic mirror, before it comes out from the very small hole at the top of the mirror. This is also a problem from project Euler: https://projecteuler.net/problem=144 | Laser |
| k-enclosing circle | Given a set of points, find the circle with the minimum radius that has at least k points inside it. There exist sophisticated algorithms which achieve lower time complexity than mine. My algorithm does a binary search on the answer, which reduces this optimization problem to the decision problem: Can you find a circle with k points inside it or not. We know that in the optimal answer, there must be a point on the boundary. Say we fix a point and say that this point is on the boundary of a circle with radius R. Then all candidate circles left lie in a circle around this point. This makes it possible to do a radial sweep line to compute the maximum number of points inside such a constrained circle. The time complexity will be O(log(precision)*n * n log(n)). This was also a task in the 2006 Central European Olympiad: antenna. See https://cses.fi/185/list/. | antenna |
| Greatest viewing angle | Given a simple polygon inside a circle, find a point on the circle which maximizes the viewing angle. Link: https://open.kattis.com/problems/hardevidence | Evidence |
| Algoland | An implementation of my solution to https://codeforces.com/problemset/problem/1070/M. A more detailed blog about this problem can be found here: https://codeforces.com/blog/entry/105126 | Algoland |
| Airport Construction | Solution to: https://open.kattis.com/problems/airport . The problem is about finding the longest straight line segment fitting inside a polygon. There are potentially lots of literal “edge” cases, but by some clever layout of the casework, it’s not that bad. | Airport |